step 1
위에서부터 셌을 때 준석이는 홀수번째 카드, 수현이는 짝수번째 카드를 가져갑니다. 홀수번째에 있는 O의 개수가 더 많으면 준석이가 이깁니다.
만약 처음부터 준석이가 이긴다면 답은 0입니다.
만약 처음부터 수현이가 이긴다면 답은 1입니다. 제일 밑 카드를 위로 올리면 홀짝이 바뀌면서 승패도 바뀌게 됩니다.
무승부일때(홀수 번째의 O와 짝수 번째의 O의 개수가 같은 경우)만 처리를 하면 됩니다.
step 2
위에서부터 2개씩 짝을 지어 봅시다. 그럼 OO, OX, XO, XX 4종류가 나옵니다. OX는 준석이가 이기는 경우, XO는 수현이가 이기는 경우입니다.
홀수 번째의 O와 짝수 번째의 O의 개수가 같기 때문에 OX의 개수와 XO의 개수가 같습니다.
만약 XO가 하나라도 있는 경우 X를 먼저 올리고 다음으로 O를 올려서 준석이가 이기게 할 수 있습니다. 즉, 이 경우 답은 최대 2입니다. 답이 2라고 정해진 것이 아닙니다.
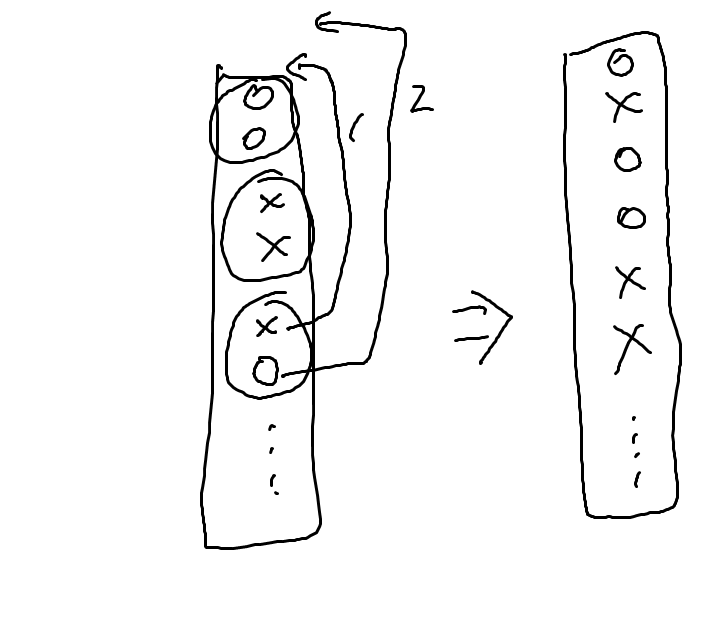
step 3
XO가 없는 경우를 생각해 봅시다. 그럼 OO와 XX만 있는 경우입니다.
OO 바로 다음으로 XX가 오는 경우가 있다고 해봅시다. 그럼 아래에 있는 X중 하나를 먼저 올리고 위에 있는 O를 위로 올리면 준석이가 이길 수 있습니다. 그럼 이 경우 역시 답은 최대 2입니다.
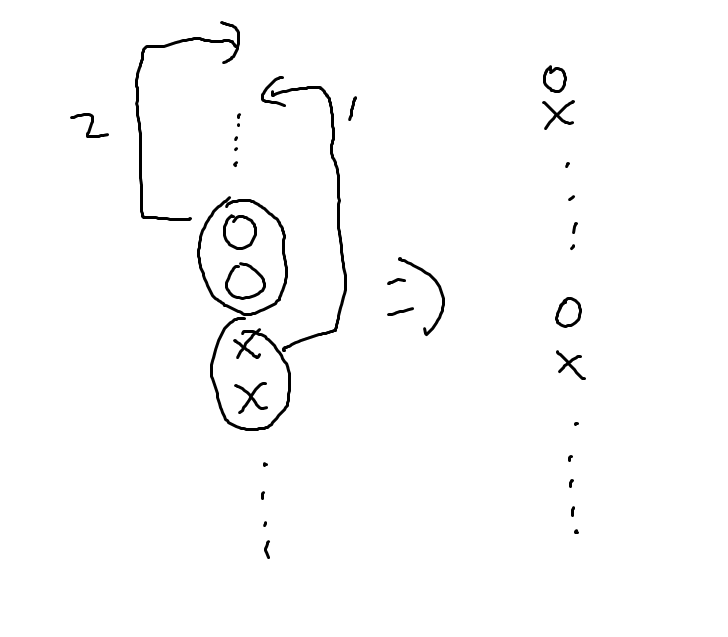
step 4
OO 바로 다음으로 XX가 오는 경우도 없다고 해봅시다. 그런 경우는 XXXXXX....XXXOOOOOO...OOOO 밖에 없습니다.
이 경우는 직접 해보면 답이 3인 것을 알 수 있습니다(O->X->O 순으로 올립니다).
이제 답이 최대 2인 경우들에 대해서만 생각해 봅시다. 이 경우들은 답이 0일수는 없으니 카드를 하나만 옯겨서 준석이를 이기게 할 수 있는지에 대한 문제로 바뀝니다. 이것은 dp로 해결할 수 있습니다.
코드
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<vector>
#include<queue>
using namespace std;
char b[3000000];
int c1[3000000], c2[3000000];
int main() {
int n, i, cnt = 0, cnt2 = 0;
scanf("%d", &n);
for (i = 1; i <= n * 2; i++) {
scanf(" %c", &b[i]);
if (i % 2 == 1 && b[i] == 'O') cnt++;
c1[i] = cnt;
if (b[i] == 'O') cnt2++;
c2[i] = cnt2;
if (n % 2 == 0 && i == n && cnt2 == 0) { printf("3"); return 0; }
}
if (cnt > n / 2) { printf("0"); return 0; }
if (n % 2 == 1 || cnt < n/2) { printf("1"); return 0; }
for (i = 2; i <= n * 2; i++) {
if (c1[n * 2] - c1[i] + (c2[i - 1] - c1[i - 1]) + (b[i] == 'O' ? 1 : 0) > n/2) {
printf("1");
return 0;
}
}
printf("2");
return 0;
}'PS - 알고리즘' 카테고리의 다른 글
| 13215 - Fish (0) | 2024.10.21 |
|---|---|
| 11025 - 요세푸스 문제 3 (0) | 2024.10.14 |
| 24520 - Meet In The Middle (0) | 2024.09.30 |
| 10479 - 따르릉 따르릉 (0) | 2024.09.23 |
| 1314 - 동굴 탐험 (0) | 2024.09.16 |



