step 1
step 2
더보기
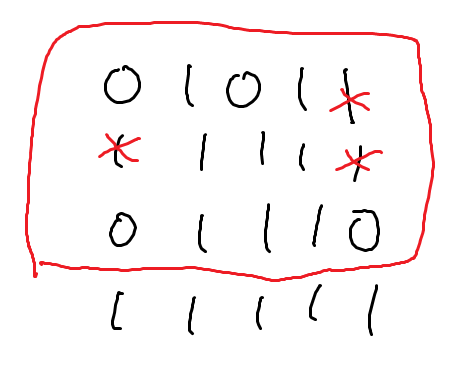
"직사각형의 밑변이 i번째 행에 있다면 만들 수 있는 직사각형의 최대 넓이는 얼마일까" 라는 질문을 모든 행에 대해서 하면 됩니다.
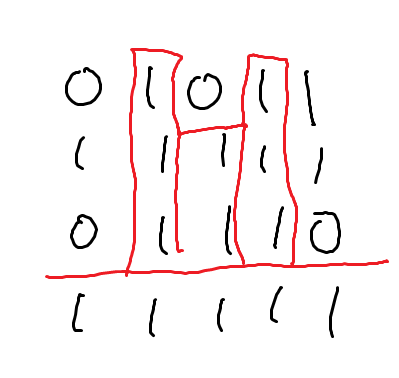
i가 정해졌다고 할 때, 0 위에 있는 1들은 아무 의미 없습니다. 그곳에 직사각형이 도달할 수 없기 때문이죠. 아래는 예제의 첫번째 케이스에서 i=3일 때입니다.

그렇다면 이 문제는 "히스토그램에서 가장 넓은 직사각형이 무엇인가"를 푸는 문제로 바뀝니다.

이 문제를 푸는데 N, 이 문제의 개수가 N이므로 N^2에 해결할 수 있습니다.
코드
더보기
#include<stdio.h>
#include<stack>
using namespace std;
stack<pair<int, int>> s;
int map[2000][2000];
int b[2000],r[2000],l[2000];
int main() {
int n, m, i,j,max=0;
while (1) {
scanf("%d%d", &n, &m);
if (n == 0 && m == 0) break;
for (i = 1; i <= n; i++) {
for (j = 1; j <= m; j++) {
scanf("%d", &map[i][j]);
if (map[i][j] == 1) b[j]++; else b[j] = 0;
while (!s.empty() && s.top().first > b[j]) {
auto p = s.top();
r[p.second] = j - 1;
s.pop();
}
s.push({ b[j],j });
}
while (!s.empty()) {
auto p = s.top();
r[p.second] = j - 1;
s.pop();
}
for (j = m; j >= 1; j--) {
while (!s.empty() && s.top().first > b[j]) {
auto p = s.top();
l[p.second] = j + 1;
s.pop();
}
s.push({ b[j],j });
}
while (!s.empty()) {
auto p = s.top();
l[p.second] = j + 1;
s.pop();
}
for (j = 1; j <= m; j++) {
if (max < (r[j] - l[j] + 1) * b[j])max = (r[j] - l[j] + 1) * b[j];
}
}
for (i = 1; i <= m; i++) b[i] = 0;
printf("%d\n", max);
max = 0;
}
return 0;
}'PS - 알고리즘' 카테고리의 다른 글
| 13209 - 검역소 (0) | 2024.06.02 |
|---|---|
| 3043 - 장난감 탱크 (0) | 2024.05.31 |
| 13537 - 수열과 쿼리 1 (0) | 2024.05.26 |
| 1055 - 끝이없음 (0) | 2024.05.26 |
| 6549 - 히스토그램에서 가장 큰 직사각형 (0) | 2024.05.24 |
