step 1
색칠되지 않은 면적을 구하는 것이지만 전체에서 색칠된 영역을 빼는 것으로 생각하고 색칠된 영역의 면적을 구하겠습니다.
$K \le 50,c[i] \le 1000$입니다. $K$를 잠시 무시하고 한번만 색칠한다 했을 때 만들어지는 영역들을 생각해 봅시다. 영역의 개수가 최대한 많아지도록 만든다면 다음과 같이 $1001 * 2$개의 영역이 만들어 질 것입니다.
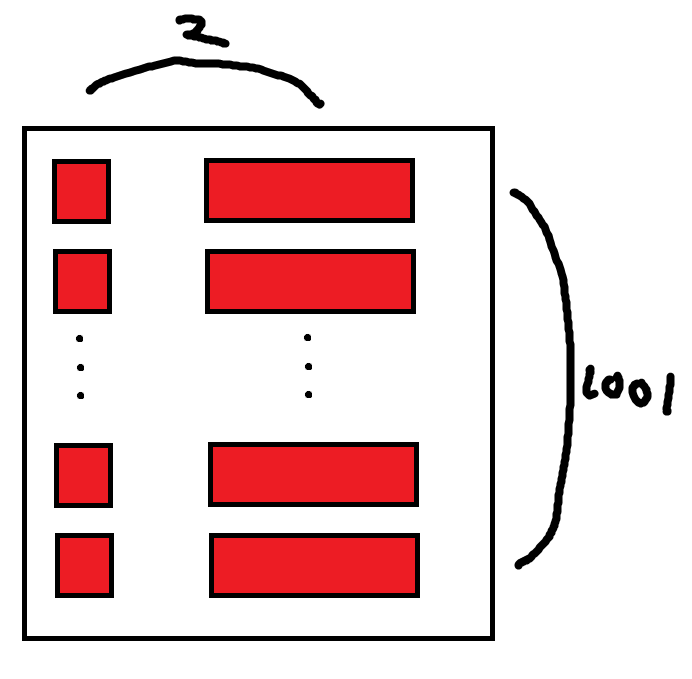
각 영역의 경계를 생각해 봅시다. 세로축과 평행한 경계가 4개, 가로축과 평행한 경계가 2002개 만들어 질 것입니다. 이를 세로 경계, 가로 경계라고 하겠습니다. $K$가 50이므로 전부 색칠하면 최악의 경우 세로 경계 200개, 가로경계 100100개가 만들어집니다. 이제 $200 * 100100$로 이 문제를 해결하면 됩니다.

step 2
예제입력 2를 이용해서 설명하겠습니다.

이 이미지에서 세로 경계는 0,1,3,5 위치에 있고 가로 경계는 1,3,5,6에 있습니다. 저희는 오른쪽으로 쭉 지나가면서 (현재 위치에서 세로로 봤을 때 색칠되어 있는 칸의 개수) * (그 상태가 유지되는 범위)를 계산할 것입니다.
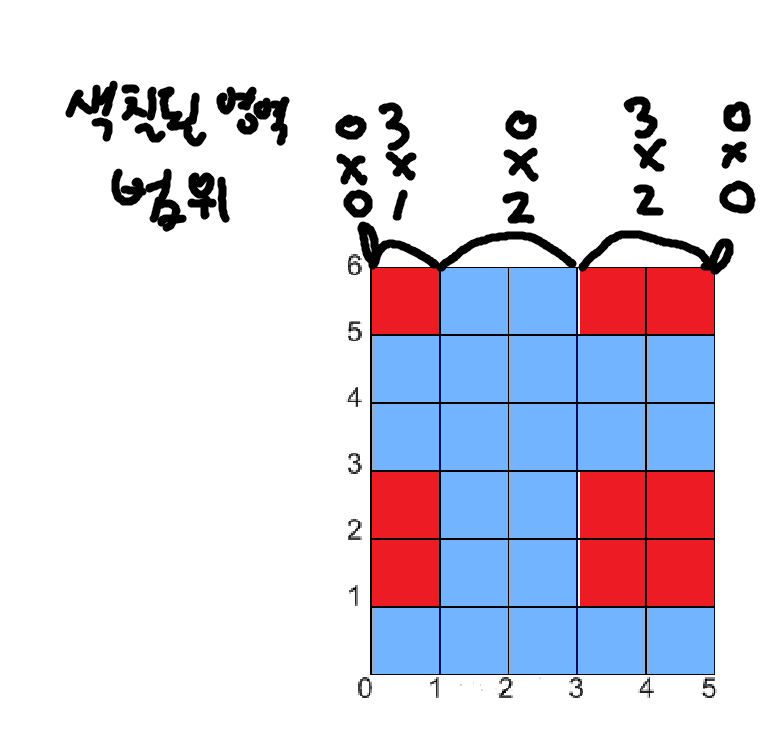
구체적으로는 다음 과정을 따릅니다.
- 왼쪽부터 시작합니다. 0이 현재 위치입니다. 오른쪽으로 천천히 이동하면서 계산을 해 줄 것입니다.
- 현재 위치 바로 다음에 있는 세로 경계를 찾습니다.
- (지금 색칠되어 있는 칸의 개수) * ((다음 세로 경계) - (현재 위치)) 를 전체 색칠된 양에 더해줍니다.
- 해당 경계에서 바뀌는 값을 적용하고 현재 위치를 다음 세로 경계로 이동시킵니다.
이 과정을 끝날 때 까지 하면 됩니다.
글로 쓰려니 잘 표현하기가 어렵네요. 예시로 시뮬레이션을 해 봅시다. 기존 예시에서 (3, 2) ~ (4, 4)에도 색칠되어 있다고 해 봅시다. 세로 경계는 0, 1, 3, 3, 4, 5입니다. 현재 위치는 0이고(초록색 세로 선) 색칠되어 있는 칸의 개수는 0개입니다.
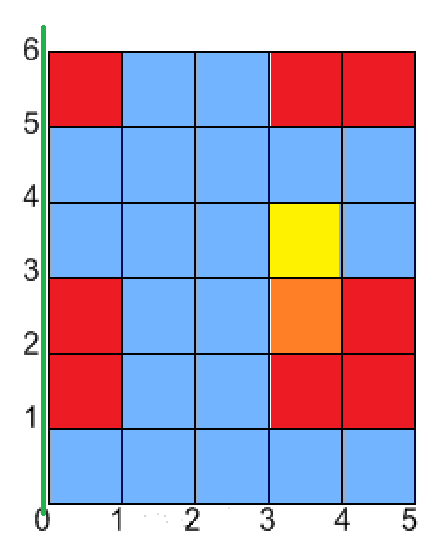
다음 세로 경계는 0입니다. 0 * (0 - 0)개의 색칠된 칸을 찾았습니다. 이제 이번 경계에서 바뀌는 값을 적용해 줍시다.
$dp$배열을 하나 만들어 줍시다. $i$번째 칸은 $i$번째 가로줄을 뜻합니다. $dp[i]$는 $i$번째 가로줄 기준으로 몇 겹이 더 색칠되는가 입니다.
$s$배열을 하나 만들어 줍시다. $s[i]$는 $dp[0] ~ dp[i]$까지의 합입니다. $s[i]$가 0이면 해당 칸에는 색이 없고 1이상이면 색이 있다는 의미입니다.
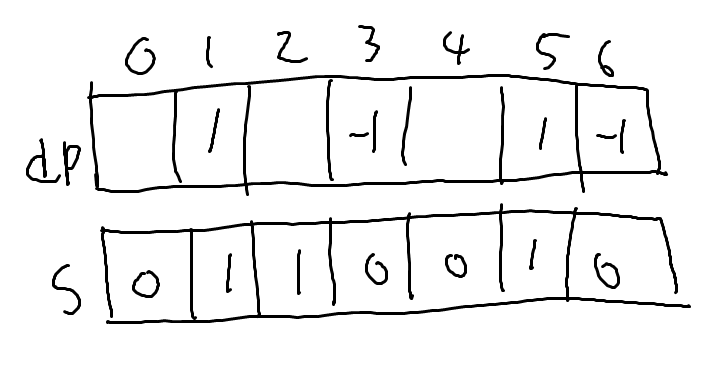
다음 세로 경계는 1입니다. 현재 3칸이 색칠되어 있고 그 상태가 1번 지속되었다는 의미이므로 3 * (1 - 0)개의 색칠된 칸을 찾은 것입니다.
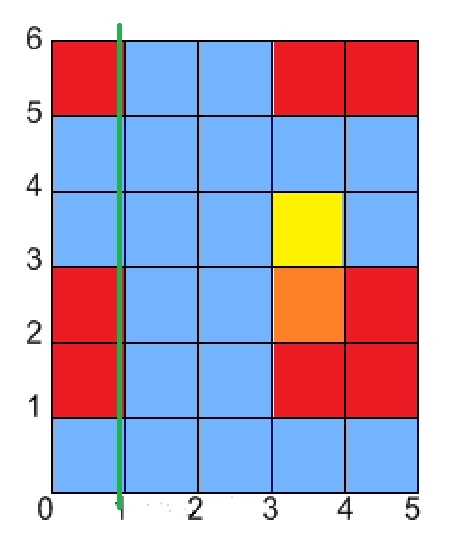
$dp$와 $s$ 배열을 갱신해 줍니다. 모든 칸이 비어 있으므로 $dp$와 $s$도 전부 0이 됩니다.
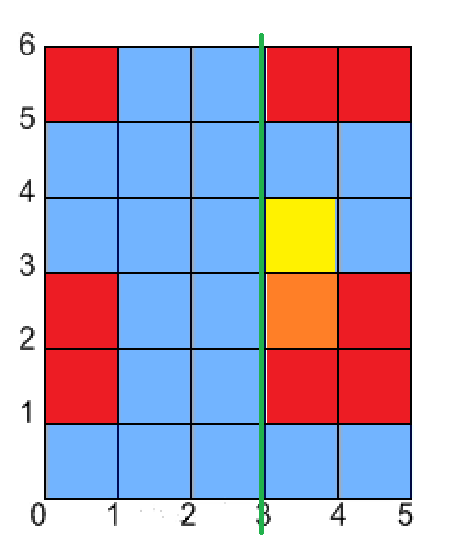
다음 세로 경계는 3입니다. 색칠된 칸이 없으므로 0 * (3 - 1)개의 색칠된 칸을 찾게 됩니다.
1, 2, 5번째 가로 경계에서 색칠되고 3, 4, 6번쨰 경계에서 색이 빠지므로 다음과 같이 됩니다.
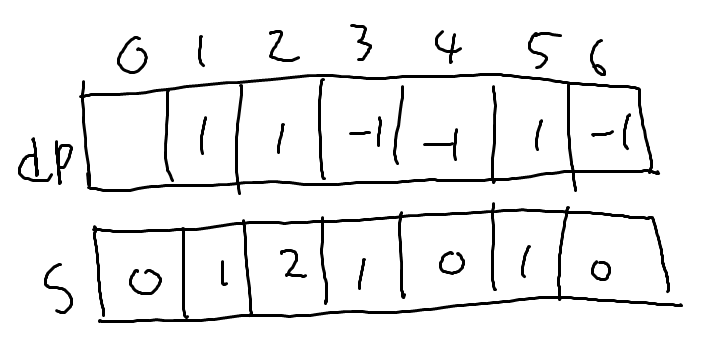
1 이상인 $s[i]$가 4개이므로 총 4개의 색칠된 칸을 찾게 됩니다.
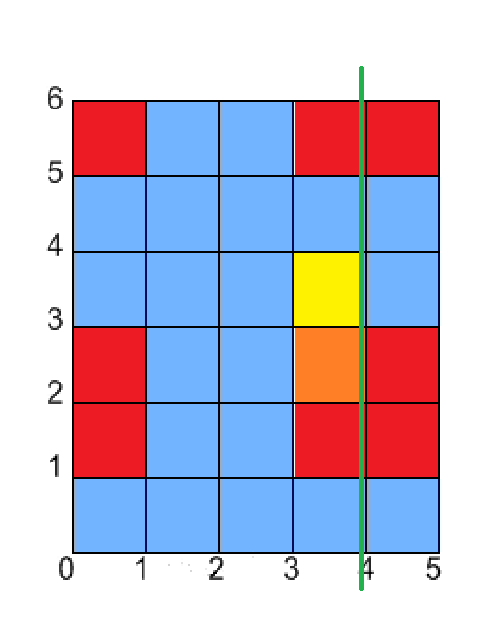
다음 세로 경계는 4입니다. 4칸이 색칠되어 있으므로 4 * (4 - 3)개의 색칠된 칸을 찾게 됩니다.

$dp$와 $s$는 이런 상태가 됩니다. 색칠된 칸은 총 3칸입니다.

마지막 세로 경계입니다. 총 3칸이 색칠되어 있으므로 3 * (5 - 4)개의 색칠된 칸을 찾게 됩니다.
step 3
$W, H$가 $10^9$입니다. 그러면 $dp, s$ 배열의 크기가 너무 커지게 됩니다. 이를 좌표 압축으로 해결할 수 있습니다.
압축한 좌표와 실제 좌표를 저장해서 '압축한 좌표 기준 1번째부처 4번째 까지 색칠되어 있으니 실제 좌표에서는 어디서부터 어디까지 색칠되어 있을까?'를 생각하면 문제를 풀 수 있습니다.
코드
#define _CRT_SECURE_NO_WARNINGS
#define ll long long
#include <cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<map>
#include<set>
using namespace std;
struct col {
ll s, e;
};
vector<col> draw[60];
struct so {
ll x, y;
inline bool operator < (const so& temp)const {
return x < temp.x;
}
}so[200000];
struct data {
ll p, i, s;
inline bool operator < (const data& temp)const {
return p < temp.p || p == temp.p && s < temp.s;
}
}po[300];
map<ll, ll> mm;
ll pcnt = 0,scnt=0,idx[200000],statt[200000];
int main() {
ll n, m, k, i, j, countt = 0;
scanf("%lld%lld%lld", &n, &m, &k);
for (j = 1;j <= k;j++) {
ll f, c, x1, y1, x2, y2, fl = 0, ts, te;
scanf("%lld%lld%lld%lld%lld%lld", &f, &c, &x1, &y1, &x2, &y2);
if (f > x1) {
ll bound = x2;
if (bound > f) bound = f;
pcnt++;
po[pcnt] = { f - bound,j,1 };
pcnt++;
po[pcnt] = { f - x1,j,-1 };
}
if (f + x1 <= n) {
pcnt++;
po[pcnt] = { f + x1,j,1 };
pcnt++;
po[pcnt] = { (f + x2 <= n ? f + x2 : n),j,-1 };
}
ts = y1;
te = y2;
for (i = 1;i <= c + 1;i++) {
draw[j].push_back({ ts,te });
scnt++;
so[scnt].x = ts;
so[scnt].y = scnt;
scnt++;
so[scnt].x = te;
so[scnt].y = scnt;
if (fl == 0) {
ll b = m / (c + 1);
ts += (b - y1) * 2;
te += (b - y2) * 2;
swap(ts, te);
}
else {
ts += y2 * 2;
te += y1 * 2;
swap(ts, te);
}
fl = 1 - fl;
}
}
sort(so + 1, so + scnt + 1);
ll tt = -1, ttt = 0;
for (i = 1;i <= scnt;i++) {
if (tt != so[i].x) ttt++;
idx[ttt] = so[i].x;
mm[so[i].x] = ttt;
tt = so[i].x;
}
sort(po + 1, po + pcnt + 1);
ll s = -1, cnt = 0;
for (i = 1;i <= pcnt;i++) {
countt += cnt * (po[i].p - s);
s = po[i].p;
ll dpo = 0, ss = -1, boo = 0,sum = 0;
cnt = 0;
for (j = 1;j <= ttt;j++) {
while (1) {
if (dpo == draw[po[i].i].size()) break;
if (boo == 0 && draw[po[i].i][dpo].s == idx[j]) { statt[j] += po[i].s; boo++; }
else if (boo==1 && draw[po[i].i][dpo].e == idx[j]) {
statt[j] -= po[i].s;
dpo++;
boo = 0;
}
else break;
}
sum += statt[j];
if (ss == -1 && sum != 0) ss = j;
else if (ss != -1 && sum == 0) {
cnt += idx[j] - idx[ss];
ss = -1;
}
}
}
printf("%lld", n * m - countt);
return 0;
}'PS - 알고리즘' 카테고리의 다른 글
| 네트워크 플로우 (0) | 2024.05.10 |
|---|---|
| 백준 30481 - Forward and Backward (0) | 2024.05.06 |
| 백준 31749 - 조작 (2) | 2024.04.27 |
| 백준 31741 - 구간 덮기 (0) | 2024.04.21 |
| 백준 19825 - Minimal Product (0) | 2024.04.14 |
