step 1
더보기
우선 정답부터 이야기하고 가겠습니다. 나온 모든 수를 xor을 한 값이 0이면 후공 승, 아니면 선공 승입니다.
놓여진 돌의 개수를 xor한 값을 그런디 넘버라고 하겠습니다. (원래 그런디 넘버의 정의는 많이 복잡하지만 이 문제에서의 그런디 넘버는 xor로 정해집니다.)
- 만약 그런디 넘버가 0이 아니라면 이 값이 0이 되도록 돌을 가져갈 수 있습니다.
- 만약 그런디 넘버가 0이라면 어떻게 돌을 가져가도 이 값은 0이 될 수 없습니다.
step 2
더보기

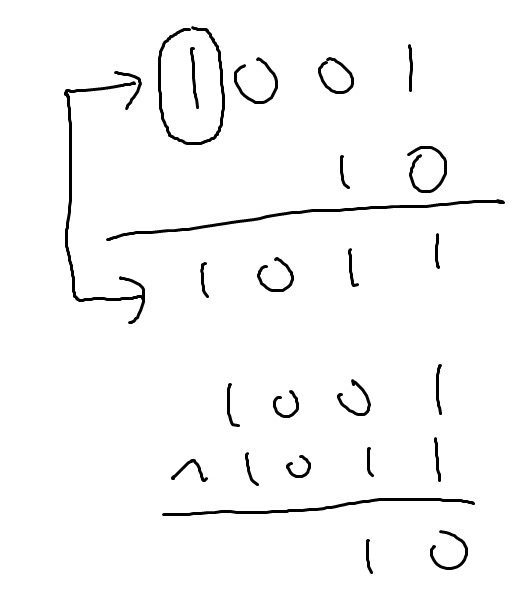
다음 예시를 봅시다.
2
9 2
이 예시에서 그런디 넘버는 9 ^ 2 = 11입니다. 그리고 9개가 있는 돌더미에서 7개를 가져가면 그런디 넘버를 2 ^ 2 = 0으로 만들 수 있습니다.
그런디 넘버$G$의 최상위 비트에 집중해 봅시다.

그럼 해당 비트를 1로 만드는 돌더미 $X$가 하나는 있다는 의미입니다. 그 돌더미 $X$와 $G$를 xor해 봅시다.
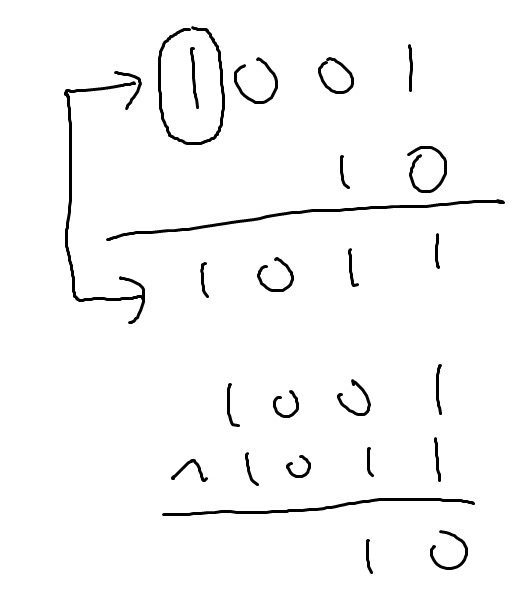
$X \oplus G$는 항상 $X$보다 작습니다. 즉, $X$가 $X \oplus G $가 되도록 돌을 가져갈 수 있다는 뜻입니다.
그럼 원래의 돌더미에서 $X$가 빠지고 $X \oplus G $가 추가되었으니 이후의 그런디 넘버는 $G \oplus X \oplus X \oplus G=0$이 됩니다.
코드
더보기
#include<stdio.h>
int main() {
int n,x,cnt=0,i;
scanf("%d", &n);
for (i = 1; i <= n; i++) {
scanf("%d", &x);
cnt ^= x;
}
if (cnt == 0) printf("cubelover"); else printf("koosaga");
return 0;
}'PS - 알고리즘' 카테고리의 다른 글
| 11401 - 이항 계수 3 (0) | 2024.07.05 |
|---|---|
| 6612 - 개미의 이동 (0) | 2024.06.27 |
| 24231 - 해석 (0) | 2024.06.26 |
| 23752 - 카드 잘 섞기 (0) | 2024.06.20 |
| 27086 - 점수 내기 (0) | 2024.06.20 |
