step 1
만약 문제의 조건을 만족하는 크기 $K*K$ 정사각형이 있다고 해봅시다. 그럼 조건을 만족하는 크기 $(K-2)*(K-2)$도 존재합니다. 물론 $(K-2)$가 1 이상이어야겠지만요.
그럼 $K$가 홀수인 경우와 짝수인 경우로 나눈 다음 각각에 대해 이분탐색이 가능합니다.
step 2
어떤 정사각형 $A$를 골라서 회전했을 때 원래 모양과 같다고 해봅시다. 그 뜻은 $A$의 중심보다 위쪽에 있는 행 하나를 오른쪽으로 읽었을 때의 값과 그에 대응되는 행을 왼쪽으로 읽었을 때의 값이 같다는 뜻입니다.
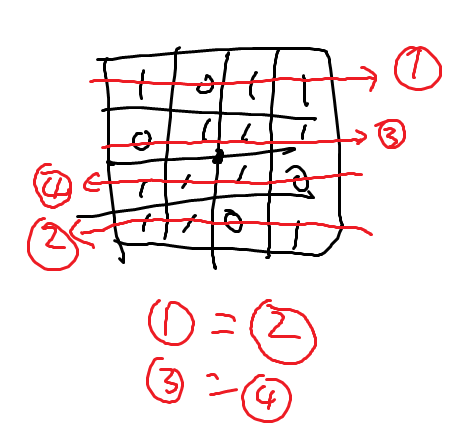
$A$의 크기가 홀수일 때는 중심의 좌우도 살펴보아야 합니다.

그럼 이분탐색으로 $K$를 정하고($\log N$) 모든 가능한 위치에 대해서 ($N*N$) 회전이 가능한지 확인하면($N*N$) $O(N^4\log N)$에 해결할 수 있습니다. 물론 불필요한 부분을 안 본다고 하면 더 줄긴 하겠지만 아직 문제를 해결하기에는 부족해 보입니다.
step 3
입력받은 값이 map에 저장되어 있다고 해봅시다.
dr[i][j] = map[i][1] ~ map[i][j]를 이진수로 생각했을 때의 값
dl[i][j] = map[i][j] ~ map[i][N]를 좌우로 뒤집은 수를 이진수로 생각했을 때의 값
을 구했다고 해봅시다.
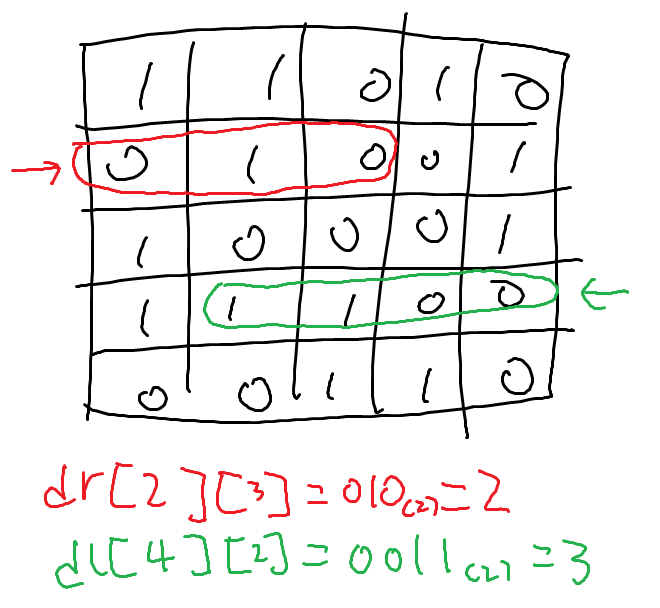
위 그림에서 $K=3$이고 중심이 $(3,3)$이라 해봅시다. 그럼 저희는 4개의 값을 알아야 합니다.
- $(2,2)~(2,4)$를 오른쪽으로 읽은 값
- $(4,4)~(4,2)$를 왼쪽으로 읽은 값
- $(3,2)~(3,2)$를 오른쪽으로 읽은 값
- $(3,4)~(3,4)$를 왼쪽으로 읽은 값
그리고 1과 4가 같은지, 2와 3이 같은지 확인하면 됩니다.
1번은 $dr[2][4]-(dr[2][1] * 2^K)$으로 구할 수 있습니다. 마찬가지로 2번은 $dl[4][2]-(dl[4][5]*2^K)$로 구할 수 있습니다.
3번과 4번 역시 같은 방식으로 구하면 됩니다.
숫자가 커지면 이 값을 구할 수 없습니다. 그러니 모든 수를 $1000000007$로 나눈 나머지를 저장해 둡니다. 숫자에 해시를 적용한다고 생각하고 해시 충돌이 일어나는지 아닌지로 체크할 수 있습니다.
코드
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<set>
using namespace std;
long long int mapp[400][400];
long long int hr[400][400],hl[400][400],M=1000000007,po[400];
int main() {
long long int n, m, i, j, k, l,eee,maxx=0;
scanf("%lld%lld", &n, &m);
eee = min(n, m);
for (i = 1;i <= n;i++) {
for (j = 1;j <= m;j++) {
scanf("%1d", &mapp[i][j]);
hr[i][j] = (hr[i][j - 1] * 2 + mapp[i][j]) % M;
}
}
for (i = 1;i <= n;i++) {
for (j = m;j >= 1;j--) {
hl[i][j] = (hl[i][j + 1] * 2 + mapp[i][j]) % M;
}
}
po[0] = 1;
for (i = 1;i <= m;i++) po[i] = (po[i - 1] * 2) % M;
long long int s = 0, e = eee / 2;
while (s < e) {
long long int mi = (s + e) / 2 + 1;
long long int r = mi * 2, ok=0;
for (i = 1;i <= n + 1 - r;i++) {
for (j = 1;j <= m + 1 - r;j++) {
for (k = 1;k <= r/2;k++) {
long long int u = hr[i+k-1][j + r - 1] - hr[i+k-1][j - 1] * po[r] % M;
if (u < 0) u += M;
long long int l = hl[i + r - k][j] - hl[i + r - k][j + r] * po[r] % M;
if (l < 0) l += M;
if (u != l) break;
}
if (k == r / 2 + 1) {
ok = 1;
break;
}
}
if (ok == 1) break;
}
if (ok == 1) s = mi; else e = mi - 1;
}
maxx = s * 2;
s = 1; e = (eee + 1) / 2;
while (s < e) {
long long int mi = (s + e) / 2 + 1;
long long int r = mi * 2 - 1, ok = 0;
for (i = 1;i <= n + 1 - r;i++) {
for (j = 1;j <= m + 1 - r;j++) {
for (k = 1;k <= r / 2 + 1;k++) {
if (k == r / 2 + 1) {
long long int u = hr[i + k - 1][j + r / 2 - 1] - hr[i + k - 1][j - 1] * po[r / 2] % M;
if (u < 0) u += M;
long long int l = hl[i + r - k][j + r / 2 + 1] - hl[i + r - k][j + r] * po[r / 2] % M;
if (l < 0) l += M;
if (u != l) break;
continue;
}
long long int u = hr[i + k - 1][j + r - 1] - hr[i + k - 1][j - 1] * po[r] % M;
if (u < 0) u += M;
long long int l = hl[i + r - k][j] - hl[i + r - k][j + r] * po[r] % M;
if (l < 0) l += M;
if (u != l) break;
}
if (k == r / 2 + 2) {
ok = 1;
break;
}
}
if (ok == 1) break;
}
if (ok == 1) s = mi; else e = mi - 1;
}
maxx = max(maxx, s * 2 - 1);
if (maxx <= 1) maxx = -1;
printf("%lld", maxx);
return 0;
}'PS - 알고리즘' 카테고리의 다른 글
| 28219 - 주유소 (0) | 2024.12.09 |
|---|---|
| 14077 - Parada (0) | 2024.12.02 |
| 25961 - 스코어보드 보기 귀찮아 (0) | 2024.11.18 |
| 12877 - 먹이 사슬 (0) | 2024.11.11 |
| 15005 - Collatz Conjecture (0) | 2024.11.04 |

