해석
$N$개의 파이프를 오른쪽에서 왼쪽으로 굴립니다. $i$번째 파이프의 반지름은 $r_i$입니다. 파이프를 다 굴렸을 때, 모든 파이프 중 벽으로부터 가장 먼 지점까지의 거리를 계산하세요
step 1
시간복잡도를 무시하면 이 문제를 어떻게 풀 수 있을까요?
$d[i]$ = 왼쪽에서 $i$번째 파이프가 벽에서 떨어진 거리
$r[i]$ = 왼쪽에서 $i$번째 파이프의 반지름
이라고 합시다. $i$번째 파이프를 굴린다고 했을 때 이 파이프가
$i-1$번째 파이프와 만날 때의 위치,
$i-2$번째 파이프와 만날 때의 위치,
...
$1$번째 파이프와 만날 때의 위치,
벽과 만날 때의 위치
를 전부 구하고 그 중 벽에서 가장 멀리 떨어진 지점이 답이 됩니다.
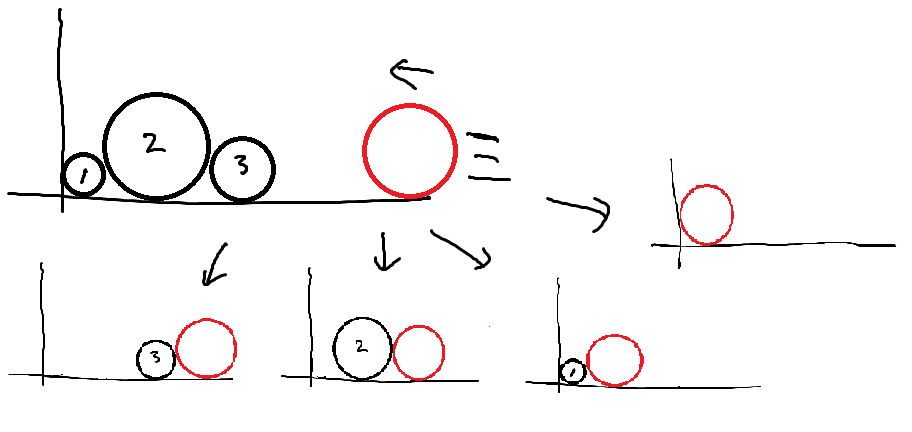
접하는 두 파이프의 반지름이 $r_1, r_2$일 때 중심 사이의 거리는 $2\sqrt{r_1r_2}$입니다.
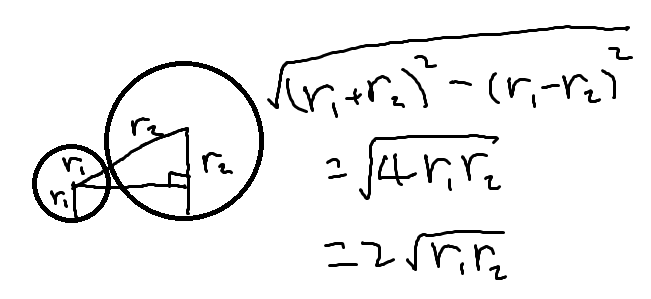
그럼 $N$개의 원에 대해서 $N$번의 연산을 하니 $O(N^2)$에 해결할 수 있습니다.
step 2
반지름이 $r$인 $i$번째 파이프를 굴렸다고 해 봅시다. 저희는 $r-1$, $r-2$, ..., 1번째 파이프와의 거리를 구할 것입니다.
만약 지금 비교하는 파이프의 반지름이 $r$보다 작거나 같다면 해당 파이프는 이 뒤에 있는 파이프에 영향을 미치지 않으니 제거해도 됩니다.
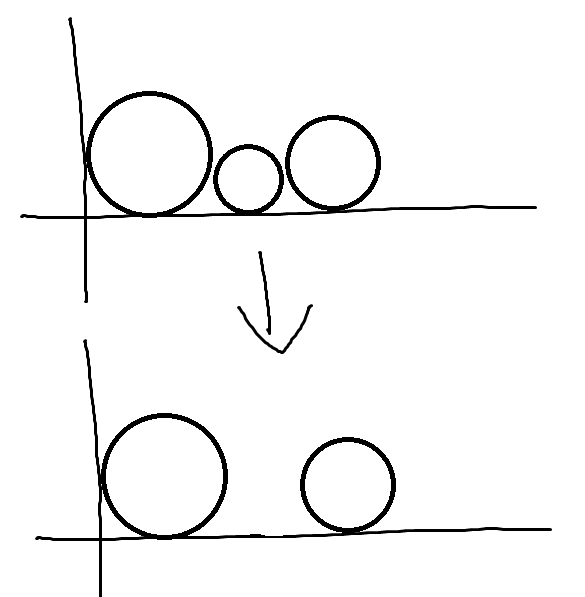
만약 지금 비교하는 파이프의 반지름이 $r$보다 크다면 이 이후에 있는 파이프와는 비교를 하지 않아도 됩니다.
비교를 할 때 마다 취할 수 있는 다음 행동은
1. 비교를 멈추거나(반지름이 $r$보다 큰 경우)
2. 파이프를 제거하거나(반지름이 $r$보다 작거나 같은 경우)
인데 파이프는 총 $N$개 있으므로 시간복잡도는 $O(N)$입니다.
코드
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
using namespace std;
double r[200000],p[200000];
int main() {
int n, i,cnt=0,j;
double maxx = 0,x,ans=0;
scanf("%d", &n);
for (i = 1; i <= n; i++) {
scanf("%lf", &x);
maxx = 0;
for (j = cnt; j >= 0; j--) {
if (j == 0) {
maxx = max(maxx, double(x));
break;
}
maxx = max(maxx, p[j] + 2 * sqrt(r[j] * x));
if (r[j] <= x) {
r[j] = 0;
p[j] = 0;
cnt--;
continue;
}
break;
}
cnt++;
r[cnt] = x;
p[cnt] = maxx;
ans = max(ans, maxx + x);
}
printf("%.10lf", ans);
return 0;
}'PS - 알고리즘' 카테고리의 다른 글
| 2244 - 민코프스키 합 (0) | 2025.01.20 |
|---|---|
| 20121 - 카드 셔플 (0) | 2025.01.13 |
| 10919 - 선물상자 (0) | 2024.12.30 |
| 18407 - 가로 블록 쌓기 (1) | 2024.12.23 |
| 2834 - 박스 정렬 (0) | 2024.12.16 |

